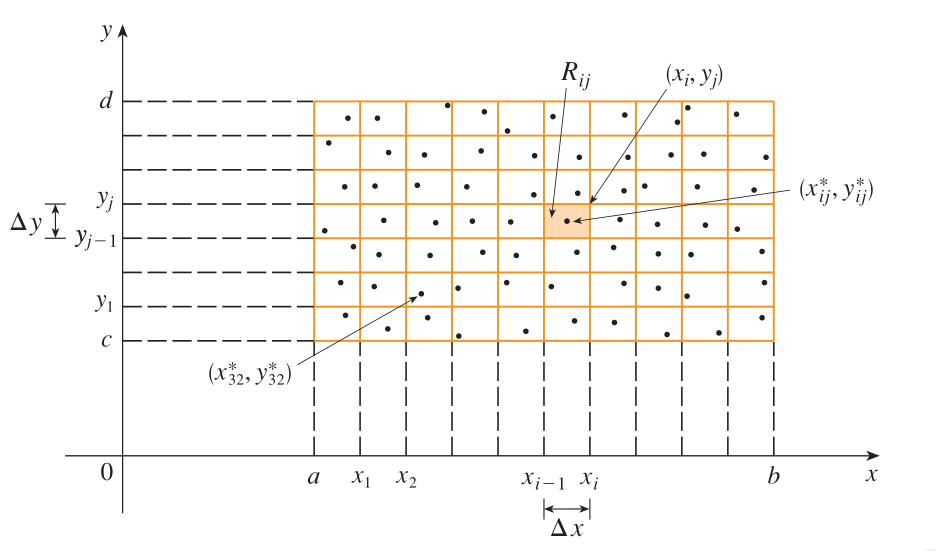
3D Riemann Sum on Rectangles
When you want to calculate the area taken up by a multivariable function in a rectangle defined by the set of points $[a,b] \times [c,d]$ which can also be written as the rectangle drawn between the points $(a,c)$ and $(b,d)$, we can split up the rectangle into smaller rectangles of area $A$. After taking a sample point from each of those rectangles, we can add up the values of those sample points to calculate an estimate of the space used. Obviously, as $A$ decreases, the estimate gets more accurate.
The Riemann sum of such a rectangle is therefore defined by:
$$ \sum_{i=0}^m\sum_{j=0}^n f(x_{ij}^, y_{ij}^) \Delta x \Delta y $$