Analysis of Merge Sort
Calculating the Big-Oh Complexity of Merge Sort is not a difficult task. There are two ways to do it, one being more intuitive and the other being more mathematical.
# Using the reccurence tree
When you draw a diagram how the merge sort algorithm calls itself recursively, you get a very intuitive yet solid proof that the algorithm’s time complexity is $O(nlog(n))$:
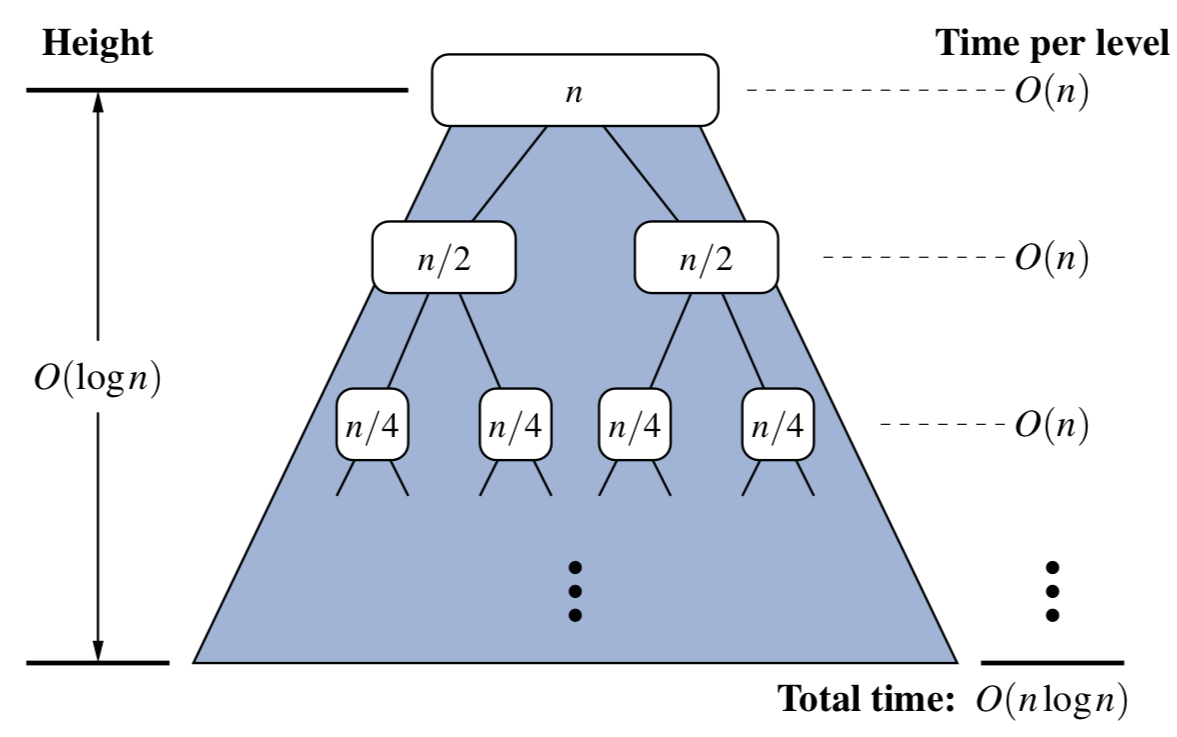
# Using its recurrence equation
Even though this approach is less intuitive I feel like this is just more solid and has its feet on the ground. Basically, when you write the recurrence equation of $t(n)$ which is the worst case running time of merge sort you get the following: $$ t(n)=\begin{cases} n \leq 1, & b \\n > 1, & 2t(\frac{n}{2}) + cn \end{cases} $$ Turning this into a closed form equation is simple: $$ t(n) = 2t(\frac{n}{2}) + cn = 2(2t(\frac{n}{4}) + \frac{cn}{2}) + cn = 4t(\frac{n}{4}) + 2cn + = 8t(\frac{n}{8}) + 3cn = 2^it(\frac{n}{2^i}) + icn $$ Since the function would continue until $\frac{n}{2^i}$ is 1 or less, the function would recurse until $i = log(n)$. Therefore, replacing i with that value yields the function:
$$ t(n) = 2^{log(n)}t(\frac{n}{2^{log(n)}}) + log(n)cn = nb + cnlog(n) $$