Big-Oh Notation
Big-Oh notation is a way of calculating the maximum time an algorithm can take relative to its input size. The two ways to calculate big-oh notation is:
# The easy way
Basically, if you have a function that consists of different versions of the 7 Important Functions the one with the highest order/the one that changes with the highest values have the highest precedence. So, for example, the function $f(n) = 2n + n^2 + 3nlog_2(n) + 2^n + 6$ has the Big-Oh $O(2^n)$ since exponential functions have the highest order.
# The big-boy mathematical way
The formal definition of Big-Oh is: $f(n)$ and $g(n)$ are both functions $\mathbb{Z}^+ \mapsto \mathbb{R}^+$. $f(n)$ is $O(g(n))$ if there is a real constant $c > 0$ and an integer constant $n_0 \geq 1$ that makes $f(n)$ less than or equal to $c \times g(n)$ for all values $n \geq n_0$. This can be written in predicate logic as such:1
$$\exists c,n_0(\forall x(x \geq n_0 \implies cg(x) \geq f(x))) \implies f(n) \in O(g(n))$$
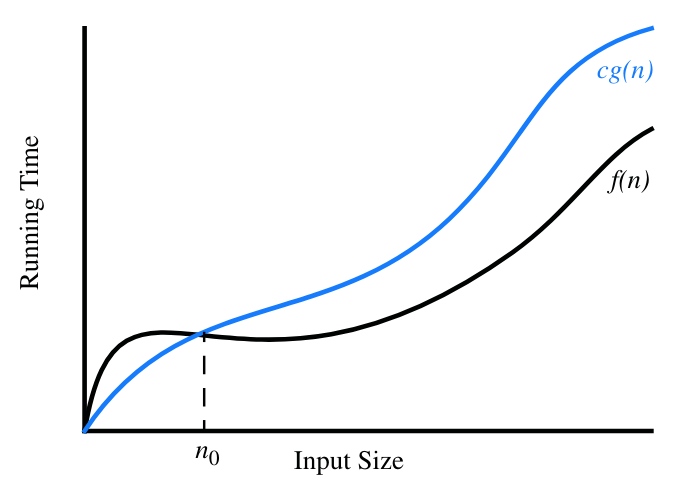
$f(n) \in O(g(n))$ is a more mathematical way of saying $f(n)$ is $O(g(n))$. ↩︎