Red-Black Tree Insertions
After inserting into a red black tree just like a BST, the newly inserted node is colored red. If its parent is black, then no property of the Red-Black tree is broken. If its parent is red however, the Red Property is broken since than a red node would have a red child. One of two cases may occur:
# The sibling of the inserted node’s parent is Black
Basically, we perform Binary Tree Restructuring operation from the newly inserted node $x$. Afterwards, we recolor $a$ and $c$ red and $b$ black. If these references are unclear, you can refer to the note on restructuring. This operation needs to be run only once, so it has $O(1)$ time complexity.
# The sibling of the inserted node’s parent is Red
In this case, a recoloring is performed as such:
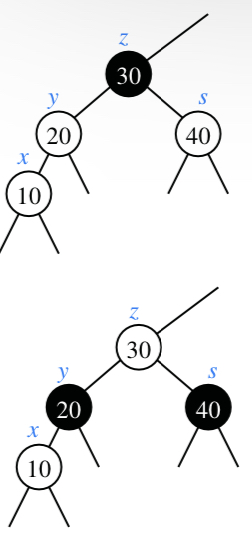This operation can cause the red property to be broken in the parent, so a recoloring is performed until we reach the root of the tree. So this operation runs in $O(log(n))$ time.