Solution of Non-Homogenous Systems

Last updated Feb 23, 2022 Edit Source

• Math linear

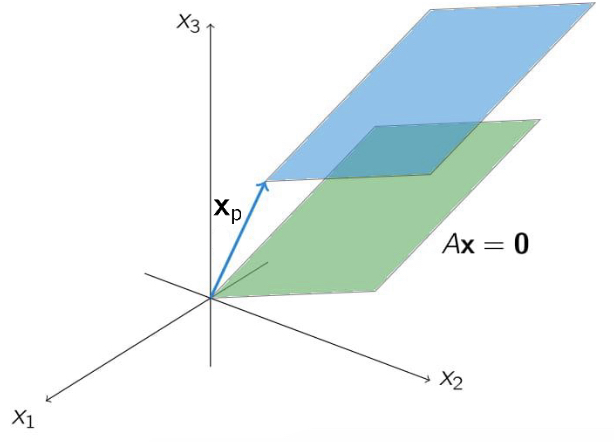
A consistent non-homogenous system $Ax=b$’s solution is $x=x_p + x_h$. In which

• $x_p$ is a special solution for the homogenous system $Ax=b$
• $x_h$ is the solution for homogenous system $Ax=0$

Let $Ax = b$ be a non-homogenous system. And let $x_p$ be a solution for $Ax = b$. This means that:

$$ Ax = b $$ $$ Ax - Ax_p = b - Ax_p $$ $$ A(x-x_p) = 0 $$