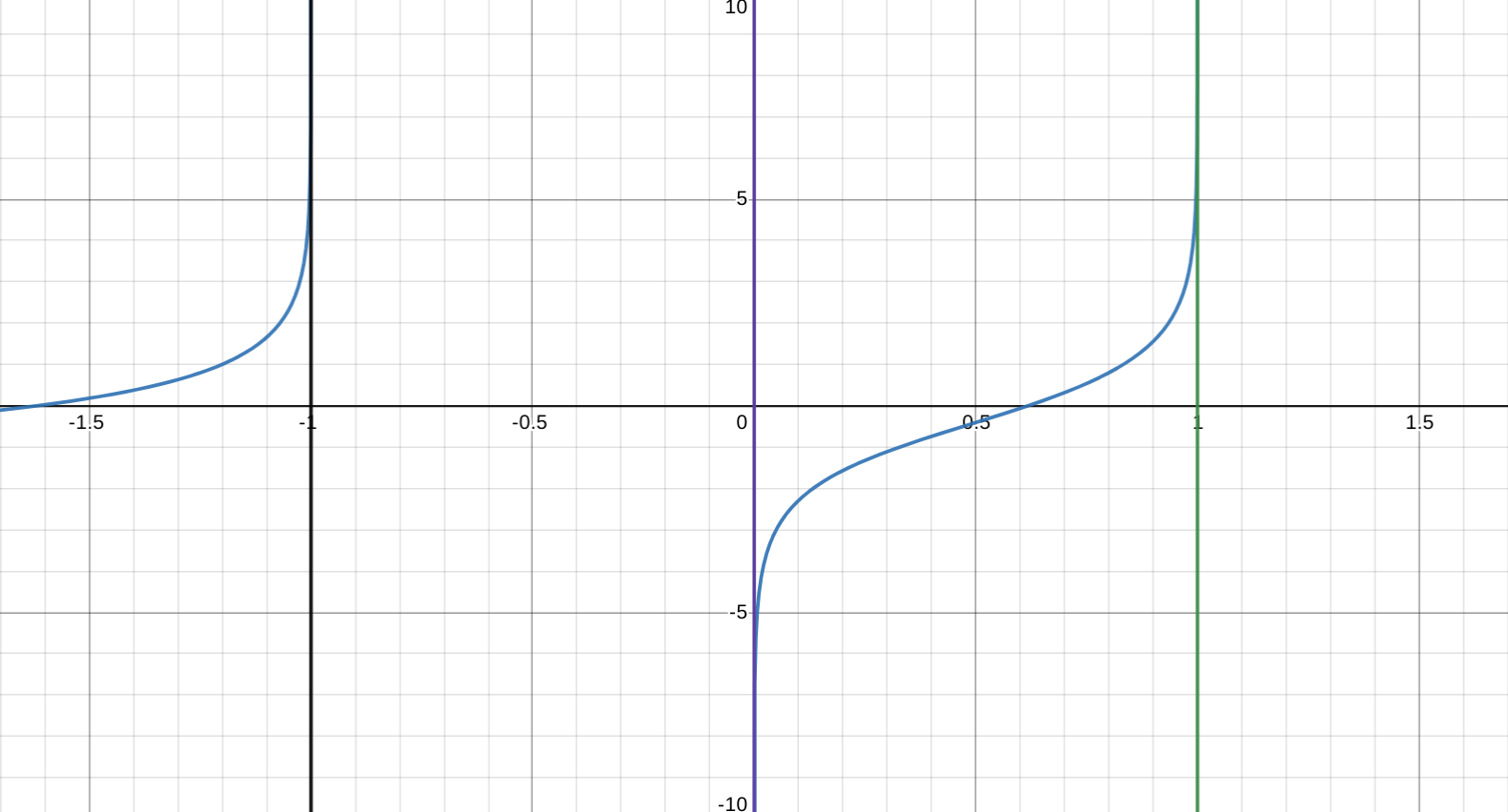
Vertical Asymptotes
Vertical asymptotes are asymptotes where the value of a function $f(x)$ is undefined at a certain point a and the function goes to infinity as x approaches x. Such asymptotes often occur in two cases:
- $f(x)$ has a logarithm: In this case, $log(x) = -\infty$ as x approaches 0, so the vertical asymptote is at the point where the inside of the logarithm is equal to 0.
- $f(x)$ has a fraction where the denominator is $g(x)$ and there is at least $x \in \mathbb{R}$ such that $g(x) = 0$. However, that value is not a vertical asymptote if it makes the numerator of that fraction a 0 as well.
An example function with asymptotes (the blue one) $f(x) = ln(\frac{x}{1-x^2})$: